Statistical Analysis Harvard Case Solution & Analysis

Statistical Analysis Case Analysis

Part 1

Assignment 1

Question 1

Part (a)

1. a = Total – Depressed

a = 38 – 3 = 35

1. b = Depressed + Not Depressed

b = 69 + 533 = 602

• c = Total – Depressed

c = 1359 – 97 = 1262

1. d = Osteoporotic + low BMD + Normal

d = 3 + 69 + 97 = 169

1. e = Osteoporotic + low BMD + Normal

e = 38 + 602 + 1359 = 1999

Part (b)

The kind of statistical test appropriate for testing the hypothesis is logistic regression.

Part (c)

T-Test Assumptions:

• The first assumption made about t-tests relates to the size of estimation. The assumption behind a t-test is that the magnitude of estimation used to analyses the data is based on a fixed or ordinal scale, such as the results of an IQ test.
• The Second assumption which is the information, results in a dispersion bend with a typical circulation and ringer development. One can provide a degree of likelihood (alpha level, level of importance, or p) as a threshold for recognition whenever a typical dispersion is anticipated. In general, a value of 5% can be anticipated.

Part (d)

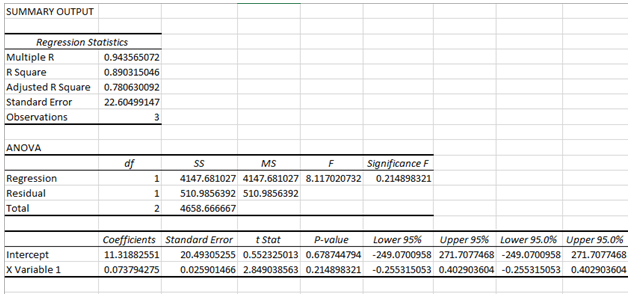
Statistical test

Part (e)

Comparing healthy, osteoporotic, and osteogenic depression ratings. 16% of patients had clinical depression, and 9% had osteoporosis. Clinically depressed persons had 40 mg/cm2 reduced BMD.

Question 2

Part (a)

Heavily drinking has been shown to increase mortality from all causes, including cardiovascular events, as opposed to light and direct alcohol usage.  Two studies from Finland and Austria demonstrated a clear link between the drinking technique known as "hitting the bottle hard" and deadly cardiac regions of localized necrosis (MI). In a study from Finland, Kauhanen et al. That is how 9 described the risk of dying from a fatal MI. was significantly more notable among guys who had at least six beers during each meeting than in those who drank fewer than three lagers. According to McElduff and Dobson12’s findings, men who drank at least nine drinks per day on one or two days out of the week had a 2.62 percent higher risk of having a serious coronary event than men who drank the same amount of alcohol over the entire week. Revealed that two to four glasses of wine, or about 20 to 40 grams of alcohol, was the threshold for significant restriction of fibrinolysis. Two glasses of wine were not enough to prevent fibrinolysis from occurring in its regular circadian manner. When drinking excessive amounts of alcohol (eight glasses of wine in one night), fibrinolysis may be inhibited till the next morning. The ethanol content of cocktails may be the cause of this effect on fibrinolysis, according to research that has shown this effect on both beer and spirits.

 Part (b)

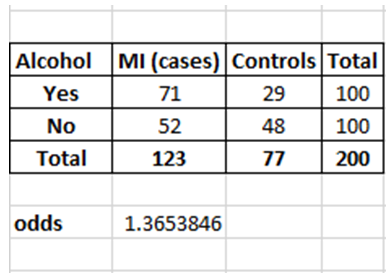
Odds of consuming alcohol among those with MI

Part (c)

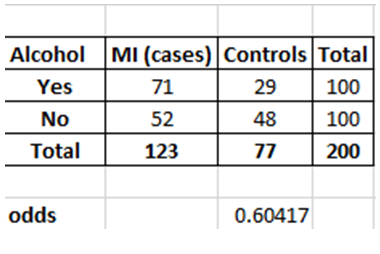
Odds of consuming alcohol among those without MI

Part (d)

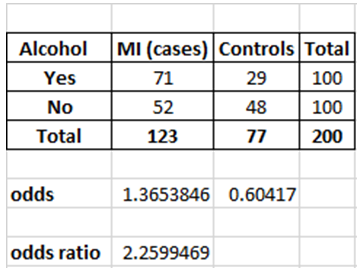
Odds ratio

Part (e)

Confidence interval

A common definition of odds is the likelihood of an event occurring divided by the probability that it will not. To put it another way, it is the percentage of victories (or wins) to defeats (or losses) (or failures).

• The likelihood of being exposed to property B is increased if the odds ratio is more than one.
• If the odds ratio is less than one, then exposure to property B has no influence on the probability of being exposed to property A.
• Odds ratios less than one are often linked with lower likelihood.

There is, however, more to the story than first meets the eye. As far as defining possible outcomes in the actual world, the odds ratio is likely to be easy. As an example, a positive odds ratio does not always mean that a person has a statistically meaningful outcome (OR). The p-values and the confidence intervals are important considerations when coming to a decision (if they know it). But even if statistical significance can be shown, the problem still persists.....

Statistical Analysis Case Analysis

This is just a sample partial case solution. Please place the order on the website to order your own originally done case solution.

Related Case Solutions & Analyses:

Airbus A3XX: Developing the Worlds Largest Commercial Jet (A) Meeting the Diversity Challenge at PepsiCo: The Steve Reinemund Era Social media: The New Hybrid Element of the Promotion Mix Cirque du Soleil–The High-Wire Act of Building Sustainable Partnerships HubSpot: Inbound Marketing and Web 2.0 Symbian Google & Apple in the Mobile Space (A) Sanctuary Soft: International Expansion Strategies U.S. Subprime Mortgage Crisis: Policy Reactions (B) The Walt Disney Company and Pixar Inc.: To Acquire or Not to Acquire HP: The Computer is Personal Again